问题
-
设总体X服从参数为λ(λ>0)的泊松分布 X1 X2 … Xn是来自X的简单随机样本 求:
-
设总体X服从(0 θ)上的均匀分布 θ>0为未知参数 X1 X2 … Xn为来自总体X的样本.试证:统计量 都是未知参数
-
设总体X服从指数分布 概率密度为( )。其中λ未知。如果取得样本观察值为x1 x2 … xn 样本均值为
-
设总体X的概率密度为其中θ>一1是未知参数 X1 X2… Xn是来自总体X的样本 则θ的矩估计量是( )。A.
-
设X1 X2 … Xn是从某总体X中抽取的一个样本 下面哪一个不是统计量( )。
-
设X1 X2 …Xn是来自总体X的一个样本 设E(X)=μ D(X)=σ2.

 其中c>0,c为已知常数;θ>1,θ为未知参数.
其中c>0,c为已知常数;θ>1,θ为未知参数.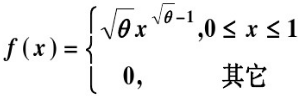 ,其中θ>1,θ为未知参数
,其中θ>1,θ为未知参数 冀公网安备 13070302000102号
冀公网安备 13070302000102号