问题
-
设随机变量X1,X2,X3相互独立,其中X1服从[0,1]上的均匀分布,X2服从正态分布N(0,22),X3服从参数为λ
-
已知随机变量X服从参数为λ的泊松分布,且P{X=0}=eˉ1,则λ=()。A、1B、-1C、0D、1/2
-
已知X服从指数分布Exp(λ) 其概率密度函数为:p(x)=λe-λx x≥0 在λ=0.1的情况
-
已知X服从指数分布Exp(λ) 其概率密度函数为:p(x)=λe-λx x≥0 在λ=0.1的情况下 P(5≤X≤20)=()。A.0.1
-
已知总体X服从[0 λ]上的均匀分布(λ未知) X1 X2 … Xn为X的样本 则( ).A.是一个统计量;B.是一个统
-
设总体X服从参数为λ(λ>0)的泊松分布 X1 X2 … Xn是来自X的简单随机样本 求:

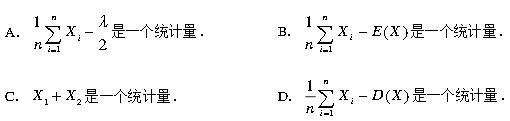
 冀公网安备 13070302000102号
冀公网安备 13070302000102号