问题
-
若函数y = f (x)在[- 1,1]上是单调函数,则使得y = f (sinx)必为单调函数的区间是()。
-
设函数f(x)的定义域为(一∞,+∞),则函数f(x)-f(-x)的图形关于()对称. A.y=x B.X轴 C.y轴 D.
-
递归函数f(x,y)定义如下:f(x,y)=f(x-1,y)+f(x,y-1) 当x>0且y>0f(x,y)=x+y 否则则f(2,1)
-
当X Y之间是1对多联系时 则存在函数依赖(36);给定函数依赖f:X—>Y和g:X—>Y 则(37)。A.X—>YB.Y—>XC.
-
设函数f(x)的定义域为(一∞ +∞) 则函数f(x)-f(-x)的图形关于( )对称. A.y=x B.X轴 C.y轴 D.
-
设函数y=f(x)的定义域为[0 1] 求:

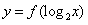 的定义域是( )。
的定义域是( )。 冀公网安备 13070302000102号
冀公网安备 13070302000102号