问题
-
设 A 为 m × n 矩阵,齐次线性方程组 AX=0 仅为零解的充分必要条件是 () 。(A) A 的行向量组线性无
-
设α β γ δ 是n 维向量 已知α β 线性无关 γ 可以由α β 线性表示 δ 不能由α β
-
下列命题中错误的是()。A.只含有一个零向量的向量组线性无关B.由3个2维向量组成的向量组线性相
-
设a1 a2 a3 β为n维向量组 已知a1 a2 β线性相关 a2 a3 β线性无关 则下列结论中正确的是( )。A.
-
设A为m×n阶矩阵 则齐次线性方程组AX=0只有零解的充分必要条件是(64)。A.A的列向量组线性无关B.A的
-
n维向量组α1 α2 … αs线性无关的充分条件是( )。 A.α1 α2 … αs均不是零向量 B.α1 α2 … αs中任意两个向量的

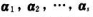 线性无关的充分必要条件是()
线性无关的充分必要条件是() 都不是零向量
都不是零向量 使得
使得
 冀公网安备 13070302000102号
冀公网安备 13070302000102号