问题
-
已知3维列向量α β满足αTβ=3 设3阶矩阵A=βαT 则( )。A.β是A的属于特征值0的特征
-
已知3维列向量α β满足αTβ=3 设3阶矩阵A=βαT 则( )。A.β是A的属于特征值0的特征
-
已知3维列向量α β满足αTβ=3 设3阶矩阵A=βαT 则( )。A.β是A的属于特征值0的特征
-
已知三维列向量α β满足αTβ=3 设三阶矩阵A=βαT 则: A.β是A的属于特征值0的特征向量B.α是
-
设A是n阶实对称矩阵 P是n阶可逆矩阵 已知n维列向量α是A的属于特征值A的特征向量 则矩阵(P-1AP)T
-
设A=(α1 α2 α3 α4)是4阶矩阵 A*为A的伴随矩阵 若(1 0 1 0)T是线性方程组Ax:O的一个基础解系 则A”

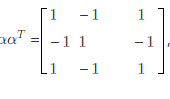 ,则αTα=?
,则αTα=? 冀公网安备 13070302000102号
冀公网安备 13070302000102号