问题
-
切比雪夫大数定律要求随机变量之间相互独立。()
-
设随机变量X1 X2 … Xn相互独立 Sn=X1+X2+…+Xn 则根据列维一林德伯格中心极限定理 当n充分大时 Sn
-
设随机变量X与Y相互独立 且分别服从参数为1与参数为4的指数分布 则P|x
-
设两个相互独立的随机变量X Y方差分别为6和3 则随机变量2X-3Y的方差为()A 51B 21C -3D 36
-
设两个相互独立的随机变量X和Y分别服从正态分布N(0 1)和N(1 1) 则( )
-
设随机变量X1 X2 … Xn …独立同分布 EXi=μ(i=1 2 …) 则根据切比雪夫大数定律 X1 X2 … Xn …依概率收敛于μ 只要X1 X2 … Xn …()。

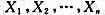 相互独立,则根据辛钦大数定律,当n充分大时,
相互独立,则根据辛钦大数定律,当n充分大时,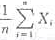 依概率收敛于其共同的数学期望,只要
依概率收敛于其共同的数学期望,只要 冀公网安备 13070302000102号
冀公网安备 13070302000102号