问题
-
设A为n阶可逆矩阵,λ是A的一个特征值,则A的伴随矩阵A*的特征值之一为()。A.λ|A|nB.λ-1|A|nC.λ|A|D.
-
设λ=1/2是非奇异矩阵A的特征值 则矩阵(2A3)-1有一个特征值为:A. 3 B.4 C.1/
-
设λ1 λ2是矩阵A 的2 个不同的特征值 ξ η 是A 的分别属于λ1 λ2的特征向量 则以下选
-
设n阶矩阵A的一个特征值为λ 则(λA-1)2+I必有特征值()。 A.λ2+1 B.λ2-1 C
-
设A为n阶可逆矩阵 λ是A的一个特征值 则A的伴随矩阵A*的特征值之一为( )。A.λ|A|nB.λ-1|A|nC.λ|A|D
-
设3阶实对称矩阵A的全部特征值为λ1=1 λ2=λ3=-1;ξ1=(1 2 -2)T为属于λ1的特征向量.求矩阵A.

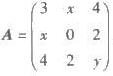 ,矩阵A的属于特征值λ1的一个特征向量为α1=(-1,0,1)T,则()。
,矩阵A的属于特征值λ1的一个特征向量为α1=(-1,0,1)T,则()。 冀公网安备 13070302000102号
冀公网安备 13070302000102号