问题
-
设随机变量X~R(0 1) Y~R(1 3) 且X与Y相互独立 求E(XY)和D(XY).
-
设A={1 2 3 4 5 6 7 8 9} R是A上的模4同余关系 求关系R。
-
设a={2 -3 1} b={1 -2 3} c={2 1 2} 向量r满足r⊥a r⊥b Prjcr=21 求r
-
设f(x)=y=x2+mx+n(m n∈R) 当y=0时 对应x值的集合为{-2 -1}(1)求m n的值(2)当x∈[-2 2]时 求函数f(x)的值域.
-
设n阶矩阵A的各行元素之和均为零 且R(A)=n-1 求齐次线性方程组Ax=0的通解。
-
设R={<a {a {a}}> <{a} a> <a a>} 求:(1)R·R.(2)domR.

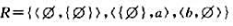 ,求:
,求: 冀公网安备 13070302000102号
冀公网安备 13070302000102号