问题
-
设随机过程 X(t)=acos(Ωt+Θ),-∞<t<+∞, 其中a是常数,随机变量Θ~U(0,2π),随机变量Ω具有概率密度f(x),设f(x)
-
设二维随机变量(X,Y)具有概率密度 则常数C=______;(X,Y)落在区域D={(x,y)|x>0,y>0,x+y≤1}内的概率为______
-
设随机变量X的概率密度为, (1) 随机变量X与函数|X|是否不相关? (2) 随机变量X与函数|X|是否相互独立?
-
设随机变量X的概率密度为求常数c并求J落在(0.3 0.7)内的概率( )。A.2 0.4B.1 0.4C.3 0.6D.4 0.6
-
设随机变量X的概率密度为 求:(1) Y=X2的概率密度;(2)Y=|X|的概率密度;(3) Y=ln|X|的概率密度.
-
设二维随机变量(X Y)具有联合概率密度f(x y)={c(x+y)0≤y≤x≤1 0其他}则常数c=()。

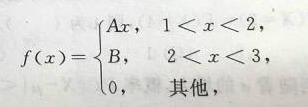 ,且
,且 冀公网安备 13070302000102号
冀公网安备 13070302000102号