问题
-
函数y =f(x)在点x=x0处取得极小值 则必有( )。A. f’(x0)=0 B. f’’(x
-
设函数f(x)在x=0的某邻域内具有二阶连续导数。且f(0)≠0 f(0)≠0 f(0)≠0.证明:存在唯一的一组实数λ
-
设函数f(x)和g(x)均在点x0的某一邻域内有定义 f(x)在x0处可导 f(x0)=0 g(x)在x0处连续 试讨论f(x)g(x)在x0
-
已知f(x)是周期为5的连续函数 它在x=0的某个邻域内满足关系式 f(1+sinx)-3f(1-sinx)=8x+0(x) 且f(x)在x=
-
设函数f(x)在x=0的某邻域内具有二阶连续导数 且f(0)≠0 f'(0)≠0 f"(0)≠0 证明:存在唯一的一组实数λ
-
设函数y=f(x)在x=0的某邻域内具有n阶导数 且f(0)=f'(0)=…=f(n-1)(0)=0 试用柯西中值定理证明: (0

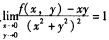 则( )。
则( )。 冀公网安备 13070302000102号
冀公网安备 13070302000102号