问题
-
已知三阶矩阵A的特征值为1,2,一3,求|A*+3A+2E|.
-
设三阶矩阵A的特征值为λ1=-1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆B.矩阵A的迹为零C.
-
设A是3阶实对称矩阵 P是3阶可逆矩阵 B=P-1AP 已知a是A的属于特征值λ的特征向量 则B的
-
已知三阶矩阵A的特征值为1 2 3 求|A3一5A2+7A|.
-
设3阶实对称矩阵A的全部特征值为λ1=1 λ2=λ3=-1;ξ1=(1 2 -2)T为属于λ1的特征向量.求矩阵A.
-
设三阶实对称矩阵A的各行元素之和均为3 向量α1=(-1 2 -1)T α2=(0 -1 1)T是线性方程组AX=0的两个解.(1)求A的

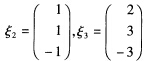 (1)求A的与λ1=2对应的特征向量. (2)求矩阵A.
(1)求A的与λ1=2对应的特征向量. (2)求矩阵A. 冀公网安备 13070302000102号
冀公网安备 13070302000102号