问题
-
定位平面斜度是指()A.上中切牙近中切角到7│7近中颊尖所连的平面与水平面的交角B.上中切牙近中
-
剖切面的选择单一剖切面,几个平行的剖切平面,几个相交的剖切面。()
-
设∑为椭球面的上半部分,点.P(x,y,z)∈∑,π为∑在点P处的切平面,ρ(x,y,z)为点O(0,0,0)到平面π的距离,求.
-
用一个平面将一个边长为1的正四面体切分为两个完全相同的部分 则切面的最大面积为()。
-
求旋转椭球面3x2+y2+z2=16上点(-1 -2 3)处的切平面与xOy面的夹角的余弦.
-
求由平面y=0 y=kx(k>0) z=0从及球心在原点 半径为R的上半球面所围成的在第一卦限内的立体的体积.
最新题目
-
收音机每台售价为90元 成本为60元.厂方为鼓励销售商大量采购.....
-
Seldom _____ this road flooded .A.have I seenB.I have seenC.I sawD.I had seen..
-
For years doctors ______ millions of patients'.....
-
No matter () the little sisters managed to round the sheep up and drive them back..
-
Once you _____ the knack of it you will have no further difficulty.A.shall haveB.had h..
-
土地革命战争后期 中国共产党确立抗日民族统一战线策略的会.....

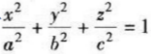 的切平面,使该切平面与三坐标面所围成的四面体的体积最小,求这切平面的切点,并求此最小体积.
的切平面,使该切平面与三坐标面所围成的四面体的体积最小,求这切平面的切点,并求此最小体积. 冀公网安备 13070302000102号
冀公网安备 13070302000102号