问题
-
直线ax-by=0与圆x2+y2-ax+by=0(a,b≠0)的位置关系是()。A.相交B.相切C.相离D.视a,b的值而定
-
小行星抛物线轨道方程可表述成y2=2px 太阳位于焦点x=p/2 y=0处。将太阳质量记为M 试求
-
直线y=ax+2和直线y=bx-3交于x轴同一点 则a与b的比值是______.
-
设抛物线y=ax2+bx+c通过点(0 0) 且当x∈[0 1]时 y≥0.试确定a b c的值 使得抛物线y=ax2+bx+c与直线x=1 y=0所
-
如图 过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A.B 交其准线于点C 若|BC|=2|BF| 且|AF|=3 则此抛物线
-
已知直线y=k(x+1)(k>0)与抛物线C:y2=4x相交于A B两点 F为C的焦点 若|FA|=2|FB| 则k= [ ]A B C D

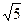 C.6 D.5
C.6 D.5 冀公网安备 13070302000102号
冀公网安备 13070302000102号