问题
-
小行星抛物线轨道方程可表述成y2=2px 太阳位于焦点x=p/2 y=0处。将太阳质量记为M 试求
-
抛物线y2=2px与直线ax+y-4=0交于两点A B 其中点A的坐标为(1 2) 设抛物线的焦点为F 则|FA|+|FB|等于( )A.7 B
-
已知双曲线x2a2-y2b2=1(a>0 b>0)的右焦点为F 右准线与一条渐近线交于点A △OAF的面积为a22(O为原点) 则两条
-
已知直线y=k(x+1)(k>0)与抛物线C:y2=4x相交于A B两点 F为C的焦点 若|FA|=2|FB| 则k= [ ]A B C D
-
椭圆x2a2+y2b2=1(a>b>0)的中心 右焦点 右顶点 右准线与x轴的交点依次为O F A H 则|FA||OH|的最大值为( )A.
-
设f:N×N→N f(<x y>)=x2+y2 说明f是否为单射的 满射的。计算f-1({0}) f({<0

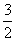 x
x 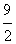 x
x 冀公网安备 13070302000102号
冀公网安备 13070302000102号