问题
-
设A是3阶矩阵 P = (α1 α2 α3)是3阶可逆矩阵 且
-
设A是3阶矩阵 P = (α1 α2 α3)是3阶可逆矩阵 且
-
设A是3阶矩阵 P = (α1 α2 α3)是3阶可逆矩阵 且
-
设A为3阶矩阵 P为3阶可逆矩阵 且若P=(α1 α2 α3) Q=(α1+α2 α2 α3) 则Q-1AQ=().
-
设A为3阶矩阵 P为3阶可逆矩阵 且P-1AP=若P=(α1 α2 α3) Q=(α1+α2 α2 α3) 则Q-1AQ=A.B.C.D.
-
设A为3阶矩阵 α1 α2为A的分别属于特征值-1 1的特征向量 向量α3满足Aα3=α2+α3. (1)证明α1 α2

 若矩阵Q=(α1,α2,α3),则Q-1AQ=()。
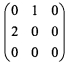
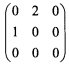
若矩阵Q=(α1,α2,α3),则Q-1AQ=()。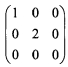

 冀公网安备 13070302000102号
冀公网安备 13070302000102号