问题
-
曲线y=e-x (x≥0)与直线x=0 y=0所围图形绕ox轴旋转一周所得旋转体的体积为( )。A
-
曲线y=e-x (x≥0)与直线x=0 y=0所围图形绕ox轴旋转一周所得旋转体的体积为( )。A
-
设曲线y=e1-x2与直线x=-1的交点为P 则曲线在点p处的切线方程是:A. 2x-y+2=0
-
曲线y=e-x(x)≥0)与直线x=0 y=0所围图形绕ox轴旋转一周所得旋转体的体积为( )。
-
设曲线y=e-x(x≥0) (1)把曲线y=e-x x轴 y轴和直线x=ξ(ξ>0)所围成平面图形绕x轴旋转一周 得一旋转体 求此旋
-
设函数y=f(x)由方程e2x+y-cos(xy)=e—1所确定 则曲线y=f(x)在点(0 1)处的法线方程为_______.

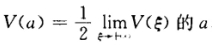 的a; (2)在此曲线上找一点,使过该点的切线与两个坐标轴所夹平面图形的面积最大,并求出该面积.
的a; (2)在此曲线上找一点,使过该点的切线与两个坐标轴所夹平面图形的面积最大,并求出该面积. 冀公网安备 13070302000102号
冀公网安备 13070302000102号