问题
-
设函数f(x)在(0 +∞)内具有二阶导数 且f(x)>0 令un=f(n)(n=1 2 …) 则
-
设函数f(u v)具有二阶连续偏导数 z=f(x xy) 则
-
设函数f(x)在x=0的某邻域内具有二阶连续导数。且f(0)≠0 f(0)≠0 f(0)≠0.证明:存在唯一的一组实数λ
-
设z=x^2+y^2 其中y=f(x)是由方程x^2-xy+y^2=1所确定的隐函数 求z对x的一次偏导和二次偏导.
-
设函数f(x)在x=0的某邻域内具有二阶连续导数 且f(0)≠0 f'(0)≠0 f"(0)≠0 证明:存在唯一的一组实数λ
-
设z=f(2x-y)+g(x xy) 其中函数f(t)二阶可导 g(u v)具有连续二阶偏导数 求。

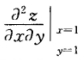 .
. 冀公网安备 13070302000102号
冀公网安备 13070302000102号