问题
-
设定义域在R上的函数f(x)=x|x|,则f(x)是A.奇函数,增函数 B.偶函数,增函数 C.奇函数,减函
-
设定义域在R上的函数,f(x)=x|x|,则f(x)是A.奇函数,增函数 B.偶函数,增函数 C.奇函数,
-
证明 可导偶函数的导函数为奇函数,而可导奇函数的导函数为偶函数.
-
已知f(x) 为连续的偶函数 则 f(x)的原函数中:( )。(A)有奇函数 (B)都是奇函数(C
-
若f(x)是连续的奇函数 证明是偶函数;若f(x)是连续的偶函数 证明是奇函数.
-
设下面所考虑的函数都是定义在区间(-l l)上的.证明: (1)两个偶函数的和是偶函数 两个奇函数的和是奇函数;

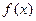 的图像关于直线
的图像关于直线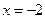 对称,当
对称,当 时,
时,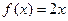 ,则
,则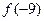 =
=  冀公网安备 13070302000102号
冀公网安备 13070302000102号