问题
-
设二阶矩过程{X(t),t∈[a,b]}的自相关函数RX(s,t)在[a,b]×[a,b]上连续,若f(t)是[a,b]上的连续函数,试证:
-
设函数f(x)在区间[a b]上连续 则下列结论中哪个不正确?
-
设函数f(x) g(x)在[a b]上连续 且在[a b]区间积分∫f(x)dx=∫g(x)dx
-
设函数f(x)在闭区间[a b]上连续 在开区间(a b)内可导 且f(x)>0.若极限存在 证明: (1)在(a b)内f
-
设函数f(x)在闭区间[0 1]上连续 在开区间(0 1)内可导 且f(0)=0 f(1)=1 证明:对于任意给定的正数a b 在开区
-
设函数f(x) g(x)在[a b]上连续 在(a b)内具有二阶导数且存在相等的最大值 f(a)=g(a) f(b)=g(b)证明:存在ξ∈(

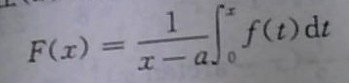 ,证明在(a,b)内F'(x)≤0.
,证明在(a,b)内F'(x)≤0. 冀公网安备 13070302000102号
冀公网安备 13070302000102号