问题
-
设X,Y,Z均为距离空间,f是X到Y中的映射,g是Y到Z中的映射,证明: (1)若f,g连续,则复合映射连续; (2)若f,g是
-
设f(x,y)为连续函数,且f(x,y)=f(y,x),证明:
-
设函数f(x)在x=0的某邻域内具有二阶连续导数。且f(0)≠0 f(0)≠0 f(0)≠0.证明:存在唯一的一组实数λ
-
设函数f(x)在[0 1]上有二阶连续导数 且f(0)=f(1)=0 f(x)≠0 x∈(0 1) 证明
-
设z=xy+xF(u) 而 F(u)为可导函数 证明.
-
设函数f(x)在[0 1]上连续 在(0 1)内可导 且证明在(0 1)内存在一点ξ 使f(ξ)=0。

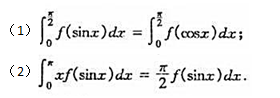
 冀公网安备 13070302000102号
冀公网安备 13070302000102号