问题
-
设{Fn}(n=1,2,…)是紧空间X中的一列闭集: 且每一个,证明:
-
设A=(aij)为n阶方阵,若任意n维非零列向量都是A的特征向量,证明:A为数量矩阵,即存在常数k,使A=kE.
-
设m与n互素 证明:mφ(n)+nφ(n)≡1(mod mn)
-
试证明: 设{fn(x}}是R1上非负渐降连续函数列.若在有界闭集F上fn(x)→0(n→∞) 则fn(x)在F上一致收敛于零.
-
设H K分别为群G的两个m与n阶子群.证明:若(m n)=1 则H ∩ K={e}.
-
设G是正有理数乘群.是整数加群.证明: 是群G到的一个同态满射.其中a b是互素的正奇数 n是整数.

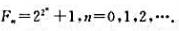 证明:对任意的n≠m,Fn与Fm互素.
证明:对任意的n≠m,Fn与Fm互素. 冀公网安备 13070302000102号
冀公网安备 13070302000102号