问题
-
设f(x)在[a b]上连续 且f(a)>0 f(b)<0 则下列结论中错误的是( ).A.至少存在一点x0∈(a b
-
设函数f(x)在闭区间[a b]上连续 在开区间(a b)内可导 且f(x)>0.若极限存在 证明: (1)在(a b)内f
-
设函数f(x)在闭区间[0 1]上连续 在开区间(0 1)内可导 且f(0)=0 f(1)=1 证明:对于任意给定的正数a b 在开区
-
设f(x)在闭区间[0 1]上连续 在开区间(0 1)内可导 且f(0)=f(1)=0 试证在(0 1)内至少存在一点 使
-
函数f(x)在[a b]上可导 且f’(x)<0是函数在该区间上单调递减的()。
-
函数f(x)在[a b]上可导 且f’(x)>0是函数在该区间上单调递增的()。

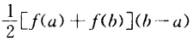 ,则
,则 冀公网安备 13070302000102号
冀公网安备 13070302000102号