问题
-
设A B为n阶对称矩阵且B可逆 则下列矩阵中为对称矩阵的是( ) A.AB-1-B-1A B.AB-1+B-1A C.B-1AB D.(AB)2
-
设n阶矩阵A满足A^2=A 则E-2A可逆且(E-2A)^-1=E-2A。()
-
设A为n(n≥2)阶可逆矩阵 交换A的第1行与第2行得矩阵B A* B*分别为A B的伴随矩阵 则 A.交换A*的第1列与第2列
-
设A为n阶非零矩阵 E为n阶单位矩阵 若A3=O 则 (A)E-A不可逆 E+A不可逆. (B)E-A不可逆 E+A可逆. (C)E-A可
-
设A为n阶可逆矩阵 则(一A)的伴随矩阵(一A)*等于( )。A.一A*B.A*C.(一1)nA*#
-
设A B C均为n阶矩阵 I为n阶单位矩阵 且ABC= I 则下列矩阵乘积一定等于I的是().

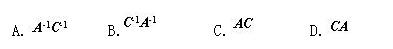
 冀公网安备 13070302000102号
冀公网安备 13070302000102号