问题
-
设f(x)具有二阶连续导数 且f(0)=0 f'(0)=0 f"(0)>0 求 其中u是曲线.y=f(x)上点(x f(x))处的切线在
-
设函数f(x) g(x)在[a b]上连续 在(a b)内具有二阶导数且存在相等的最大值 f(a)=g(a) f(b)=g(b)证明:存在ξ∈(
-
设函数z=f(xy yg(x)) 函数f具有二阶连续偏导数 函数g(x)可导且在x=1处取得极值g(1)=1.求.
-
设z=f(2x-y)+g(x xy) 其中函数f(t)二阶可导 g(u v)具有连续二阶偏导数 求。
-
设函数f(x) g(x)在[a b]上连续 在(a b)内具有二阶导数且存在相等的最大值 f(a)=g(a) f(b)=g(b)
-
设f(u)具有二阶连续导数 且g(x y)=.

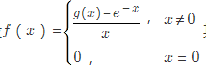 ,其中g(x)具有二阶连续导数,且g(0)=1,g'(0)=-1
,其中g(x)具有二阶连续导数,且g(0)=1,g'(0)=-1 冀公网安备 13070302000102号
冀公网安备 13070302000102号